CS 61B | Part 14 | Compression, P = NP?, Conclusions

Compression

Model #1: Algorithms Operating on Bits

Model #2: Self-Extracting Bits

Prefix Free Codes

By default, English text is usually represented by sequences of characters, each 8 bits long, e.g. ‘d’ is 01100100.

word	binary	hexadecimal
dog	01100100 01101111 01100111	64 6f 67

Easy way to compress: Use fewer than 8 bits for each letter.

• Have to decide which bit sequences should go with which letters.
• More generally, we’d say which codewords go with which symbols.

Morse Code:

M is prefix of G. We can see this in Morse Code Tree:

Alternate Strategy: Avoid ambiguity by making code prefix free.

• Prefix-Free Example #1:

  A prefix-free code is one in which no codeword is a prefix of any other.

  

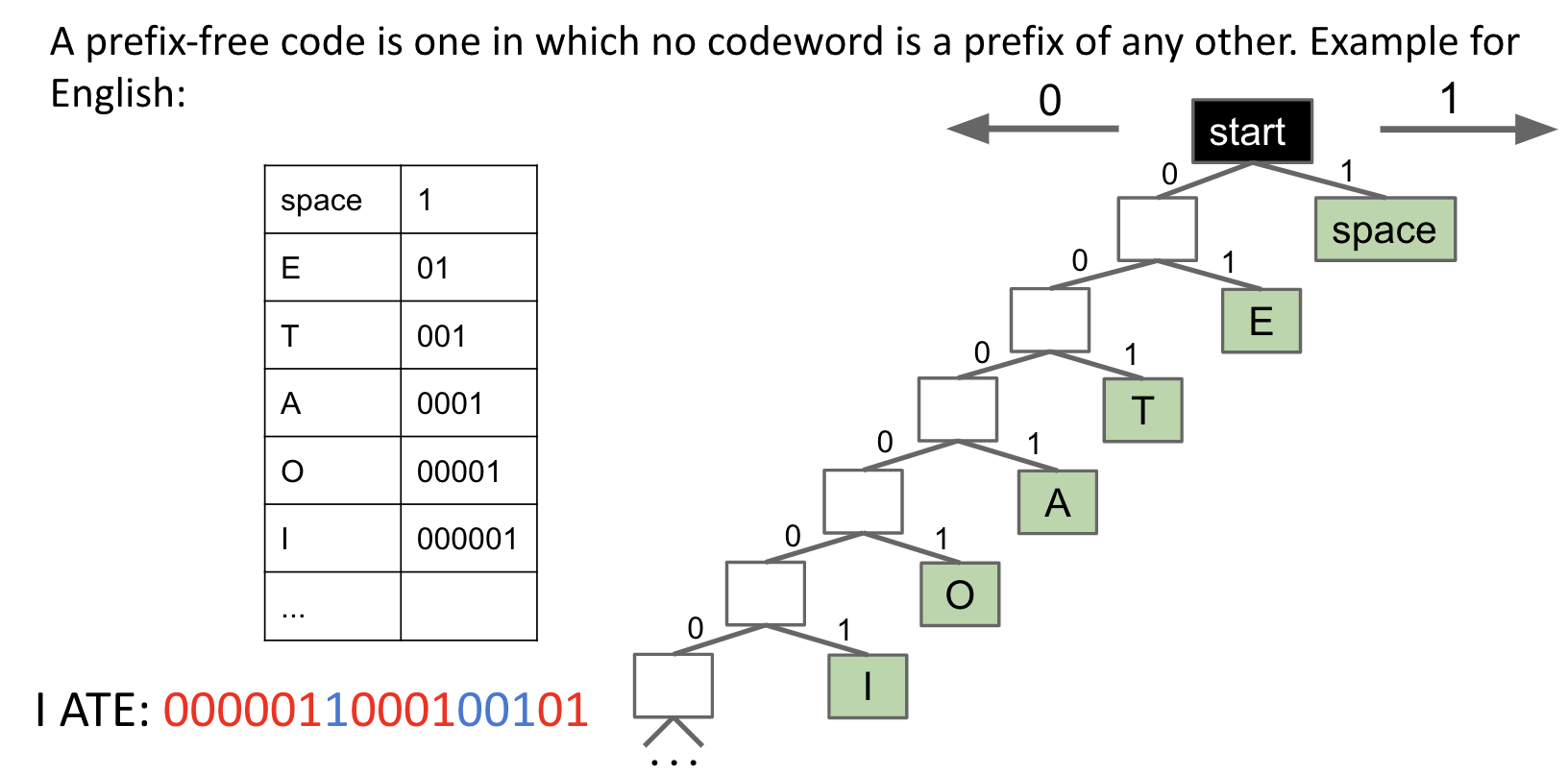
  Note:

  • I ATE could be decoded with no pauses.
  • Characters are always leaves.

• Prefix-Free Example #2:

  

Code Calculation Approach

Observation: We can see that some prefix-free codes are better for some texts than others.

Shannon-Fano Codes

• Count relative frequencies of all characters in a text.
• Split into left and right halves of roughly equal frequency.

我爸在左边。

Conclusion: Shannon-Fano coding is NOT optimal. Does a good job, but possible to find better codes.

Huffman Coding

Calculate relative frequencies $f$.

• Assign each symbol to a node with weight = relative frequency $f$.
• Take the two smallest nodes and merge them into a super node with weight equal to sum of weights.
• Repeat until everything is part of a tree.

Example:

Efficiency:

How many bits per symbol do we need to compress a file with the character frequencies listed below using the Huffman code that we created?

Another Comparison Example:

But remember the trade-off: We can only represent the particular characters.

Huffman vs. Shannon-Fano:

Shannon-Fano code below results in an average of 2.31 bits per symbol, whereas Huffman is only 2.3 bits per symbol.

Huffman coding is strictly better than Shannon-Fano coding. There is no downside to Huffman coding.

Data Structures

Question #1: For encoding (bitstream to compressed bitstream), what is a natural data structure to use? Char are just integers, e.g. ‘A’ = 65. Two approaches:

• Array of BitSequence[], to retrieve, can use character as index.
• How is this different from a HashMap<Character, BitSequence>? Lookup consists of:
  • Compute hashCode
  • Mod by number of buckets
  • Look in a linked list if collision happens

Compared to HashMaps, Arrays are faster, but use more memory if some characters in the alphabet are unused.

Question #2: For decoding (compressed bitstream back to bitstream), what is a natural data structure to use?

Hint: Prefix Operations!

Since we need to look up longest matching prefix, an operation that Tries excel at.

Usage In Practice

Two possible philosophies for using Huffman Compression:

• Philosophy 1: Build one corpus per input type.
  • For each input type, assemble huge numbers of sample inputs for that category. Use each corpse to create a standard code.

    java HuffmanEncodePh1 ENGLISH mobydick.txt
    java HuffmanEncodePh1 BITMAP horses.bmp

  • Con: Will result in suboptimal encoding.
• Philosophy 2: For every possible input file, create a unique code just for that file. Send the code along with the compressed file.

  java HuffmanEncodePh2 mobydick.txt
  java HuffmanEncodePh2 horses.bmp

  • Require you to use extra space for the codeword table in the compressed bitstream.

In practice, Philosophy 2 is used in the real world.

Note: In step 1, consider each b-bit symbol (e.g. 8-bit chunks, Unicode characters, etc.) of X.txt, counting occurrences of each of the $2^b$ possibilities, where $b$ is the size of each symbol in bits.

Code (algs4): Huffman.java

Compression Theory

There are many other approaches:

• Run-length encoding: Replace each character by itself concatenated with the number of occurrences.
  • Rough Idea: XXXXXXXXXXYYYYXXXXX -> X10Y4X5
• LZW: Search for common repeated patterns in the input.

General Idea: Exploit redundancy and existing order inside the sequence. Sequences with no existing redundancy or order may actually get enlarged.

SuperZip:

Suppose an algorithm designer says their algorithm SuperZip can compress any bitstream by 50%. Why is this impossible?

Argument 1: If true, they’d be able to compress everything into a single bit.

Argument 2: There are far fewer short bitstreams than long ones. Guaranteeing compression even once by 50% is impossible. For example:

• There are $2^{1000}$ 1000-bit sequences.
• There are only $1 + 2 + 4 + \ldots + 2^{500} = 2^{501} - 1$ bitstreams of length $\leq 500$.
• In other words, you have $2^{1000}$ things and only $2^{501} - 1$ places to put them.
• Of our 1000-bit inputs, only roughly $1$ in $2^{499}$, that is $\frac{2^{501} - 1}{2^{1000}}$, can be compressed by 50%.
• It shows that most data is incompressible.

Self-Extracting Bits

As a model for the decompression process, let’s treat the algorithm and the compressed bitstream as a single sequence of bits.

• Imagine storing the compressed bitstream as a byte[] variable in a .java file.

• algorithm + compressed bitstream –> Interpreter

Example: HugPlant

To keep things conceptually simpler, let’s package the compressed data plus decoder into a single self-extracting .java file.

Major operating systems have no idea what to do with a .huf file, we have to send over the 43,400 bits of Huffman .java code as well.

LZW

It is named for inventors Limpel, Ziv, Welch. It was once a hated algorithm because of attempts to enforce licensing fees. Patent expired in 2003.

Compressing:

Key Idea: Each codeword represents multiple symbols.

• Start with trivial codeword table where each codeword corresponds to one ASCII symbol.
• Every time a codeword $X$ is used, record a new codeword $Y$ corresponding to $X$ concatenated with the next symbol.

Neat fact: You don’t have to send the codeword table along with the compressed algorithm. It is possible to reconstruct codeword table alone.

Decompressing:

Key Idea: After processing each codeword, add the codeword that would have been added by the previous character.

Lossy Compression

Most media formats lose information during compression process like .JPEG, .MP3, and .MP4.

Basic Idea: Throw away information that human sensory system does not care about.

Examples: Audio with high frequencies, video with subtle gradations of color (low frequencies).

Summary:

Huffman coding: Represent common symbols as codeword with fewer bits.

• Use something like Map<Character, BitSeq> for compression.
• Use something like TrieMap<Character> for decompression.

LZW: Represent multiple symbols with a single codeword.

• Use something like TrieMap<Integer> for compression.
• Use something like Map<Character, SymbolSeq> for decompression.

P = NP?

It’s a question posed by Stephen Cook in 1971: Are all NP problems also P problems? In other words, are all problems with efficiently verifiable solutions also efficiently solvable?

One reason to think yes:

Easy to check any given answer. Maybe with the right pruning rules you can zero in on the answer.

How do we know X can be turned into a longest paths problem?

Short Answer: It’s a problem in the complexity class NP and therefore can be reduced to any NP complete problem, including longest paths.

Two important classes of yes/no problems:

• P: Efficiently solvable problems.
  • Is this array sorted?
  • Does this array have duplicates?
• NP: Problems with solutions that are efficiently verifiable (quickly check if it is true).
  • Is there a solution to this 3SAT problem?
  • In graph G, does there exist a path from $s$ to $t$ of weight $> k$?

Examples of problems not in NP:

• Is this the best chess move I can make next?
  • Hard to verify.
• What is the longest path?
  • Not a yes/no question.

Totally Shocking Fact:

Every single NP problem reduces to 3SAT. In other words, any decision problem for which a yes answer can be efficiently verified can be transformed into a 3SAT problem (“efficient” here mean polynomial time).

Almost Like Gods

Poll:

NP Complete Problems:

Fun Fact: Mathematical Proofs Are in NP! If P = NP, then mathematical proof can be automated.

P = NP means checking a proof is roughly as easy as creating the proof.

Millenium Prize Problems:

Even More Impressive Consequences:

Does Short = Comprehensible?

Scott Aaronson earlier made an implicit conjecture that a short program will also be comprehensible. However, there are also reasons to suspect that simplicity might not indicate comprehensibility. Short problems can produce surprisingly complex output.

For example: Fractals.

Also, music can be from very short programs.

Course Summary

Some Examples of Implementations for ADTs:

Array-Based Data Structures:

• ArrayLists and ArrayDeque
• HashSets, HashMaps, MyHashMap: Array of buckets
• ArrayHeap (tree represented as an array)

Linked Data Structures:

• Lined Lists
  • LinkedList, IntList, LinedListDeque, SLList, DLList
• Trees: Hierarchical generalization of a linked list. Aim for bushiness.
  • TreeSet, TreeMap, BSTMap, Tries
• Graphs: Generalization of a tree.

Tractable Graph Problems and Algorithms:

Searching and Sorting: