Reference: LeetCode
Difficulty: Easy

Nice Video: Finding Prime numbers - Sieve of Eratosthenes

Problem

Count the number of prime numbers less than a non-negative number n.

Example: 

1
2
3
Input: 10
Output: 4
Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.

Analysis

Methods:

  1. Brute-Force

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    public int countPrimes(int n) { // < n
      if (n <= 2) return 0; // 0, 1 are not primes
      int count = 0;
      for (int i = 2; i < n; ++i) {
        if (isPrime(i)) {
          count += 1;
        }
      }
      return count;
    }
    private boolean isPrime(int num) { // O(N)
      if (num <= 1) return false;
      for (int i = 2; i * i <= num; ++i) {
        if (num % i == 0) return false;
      }
      return true;
    }

    Time: $O(N^2)$
    Space: $O(1)$

  2. Using Square Root

    • If n is not prime, n = a x b, a <= b => a <= sqrt(n).
    • Note:
      • Use i * i <= num rather than i <= Math.sqrt(num), since the former one is faster.
      • Use i * i <= num instead of i * i < num, the latter one is incorrect.
        1
        2
        3
        4
        5
        6
        7
        private boolean isPrime(int num) { // O(sqrt(N))
          if (num <= 1) return false;
          for (int i = 2; i * i <= num; ++i) {
            if (num % i == 0) return false;
          }
          return true;
        }
        Time: $O(N\sqrt{N}) = O(N^{1.5})$
        Space: $O(1)$

  3. Sieve of Eratosthenes

    • The basic idea is to remove primes’ multiples till $n - 1$.
    • Some Optimizations:
      • We don’t need to process potential primes larger than $\sqrt{n}$, since those non-prime numbers which are larger than $\sqrt{n}$ have already been struck off by the multiples of the primes less than or equal to $\sqrt{n}$.
      • Each multiple j of a prime i can start from i * i since the smaller multiples have been struck off by other smaller primes.
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        17
        18
        19
        20
        21
        22
        23
        24
        public int countPrimes(int n) { // O(N loglogN)
          if (n <= 2) { // 0 and 1 are not primes
            return 0;
          }
          boolean[] isPrime = new boolean[n];
          for (int i = 2; i < n; ++i) isPrime[i] = true; // Init all as primes
          // Loop's ending condition is i * i < n instead of i < sqrt(n)
          // to avoid repeatedly calling an expensive function sqrt().
          
          // Sieve
          for (int i = 2; i * i < n; ++i) { // for potential prime multiples
            if (isPrime[i] == false) continue;
            for (int j = i * i; j < n; j += i) { // upper bound is < n, because n is not included
              isPrime[j] = false;
            }
          }
          
          // count
          int count = 0;
          for (int i = 2; i < n; ++i) {
            if (isPrime[i]) count += 1;
          }
          return count;
        }
        Time: $\frac{N}{2} + \frac{N}{3} + \frac{N}{5} + \ldots = O(N\log{\log{N}}) \sim O(N)$
        Space: $O(N)$

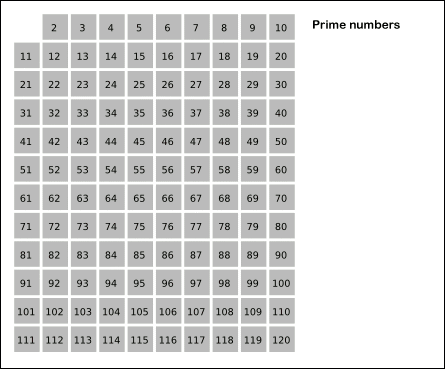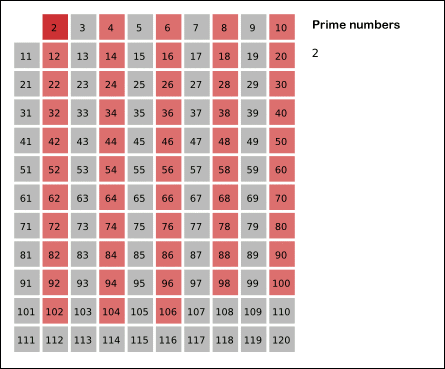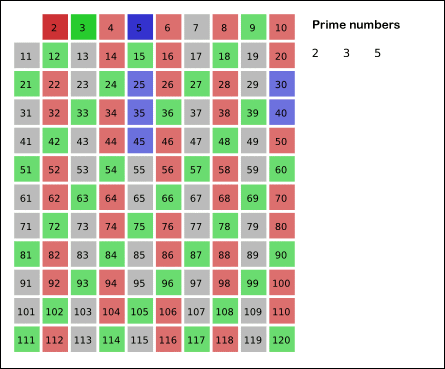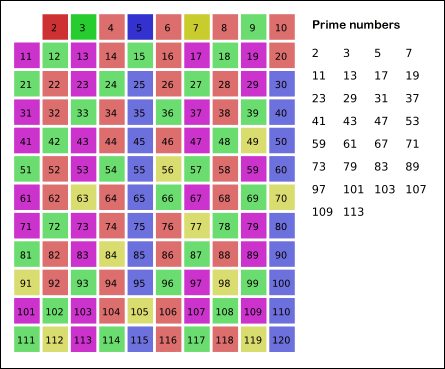
Sieve of Eratosthenes: algorithm steps for primes below 121. “Sieve of Eratosthenes Animation” by SKopp is licensed under CC BY 2.0.