陷入多元微积「危机」分时写的笔记

Junhao Wang

2018-01-27

Math

多元函数

多元函数：输入由多个变量构成的函数，是一个空间的点到另一个空间的点的映射。虽然输出由多个变量构成的函数也可被称为多元函数，但是它们通常被称为向量值函数。

导数（Derivatives）: the rate of change of a function as you slightly tweak its input.
积分（Integrals）: how to add together infinitely infinitesimal quantities that make up a function’s output.

研究多元函数可以告诉我们在不同方向上函数值的变化情况，以及这些变化间的关系。

向量值函数（Vector-valued Functions or Vector Functions）

定义域：标量 or 矢量
值域：矢量

可用向量场（Vector Field）表示该函数：$f(x,y)=\left[\begin{aligned}F(x,y)\ G(x,y)\end{aligned}\right]$

颜色表示向量的长度

可视化（Visualization）

在多元函数中，我们并不总是对函数进行可视化，而且并不总是将导数看作是斜率（Slope）。但是，我们仍然可以通过以下几种方式进行可视化：

图形：通常只适用于二对一的函数，如 $f(x,y)=e^{-(x^2+y^2)}$、$f(x,y)=\cos(x)\sin(y)$。

在实际中，对于维度较高的函数如 $f(x,y,z)=x^2+y^2+z^2$，人们通常先研究 $f(x,y)=x^2+y^2$ 的性质（概念原型），并将发现的一些性质推广到原始的高维函数中。
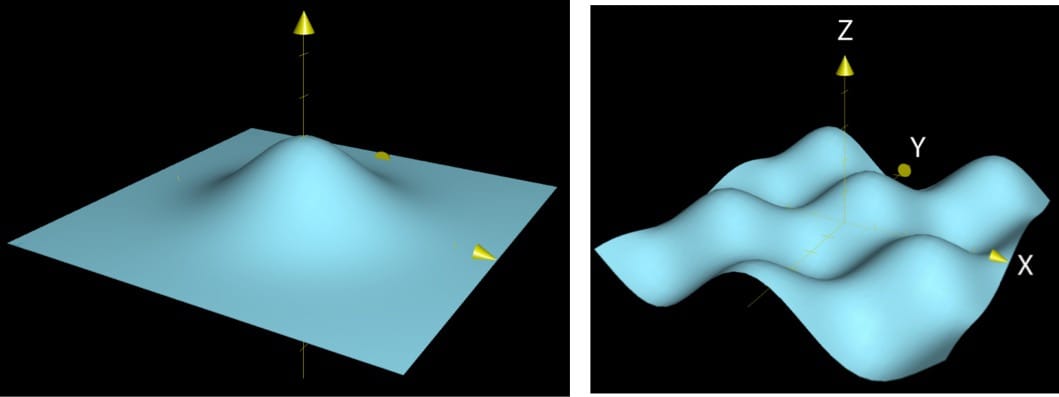
等高线图：该图只显示输入空间，适用于二对一的函数。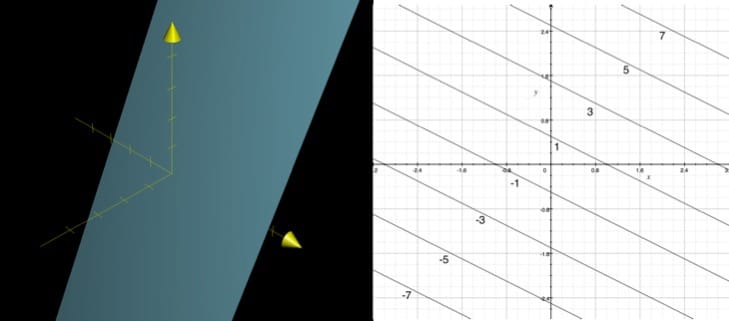
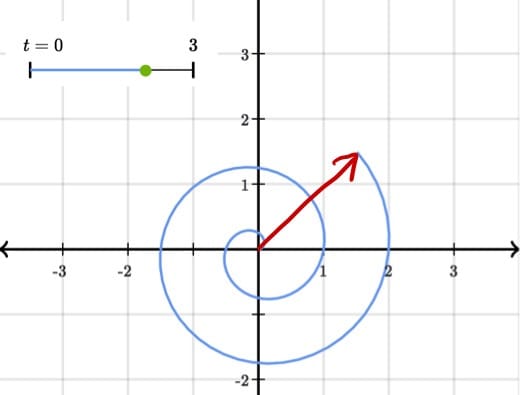
参数曲线/平面：适用于输出空间维度大于输入空间的情况，如 $f(t)=\left[\begin{aligned}2t\ 3t \end{aligned}\right]$、$f(t)=\left[\begin{aligned}\sin(t)\ \cos(3t) \ 3t \end{aligned}\right]$。
- 一个输入：$f(t)=\left[\begin{aligned}t\cos(2\pi t)\ t\sin(2\pi t)\end{aligned}\right]$
- 两个输入：$f(s,t)=\left[\begin{aligned}t^3-st\ s-t\ s+t\end{aligned}\right]$
向量场：适用于输入空间维度与输出空间维度相等的函数，如 $f(x,y)=\left[\begin{aligned}1\ y^2-y\end{aligned}\right]$。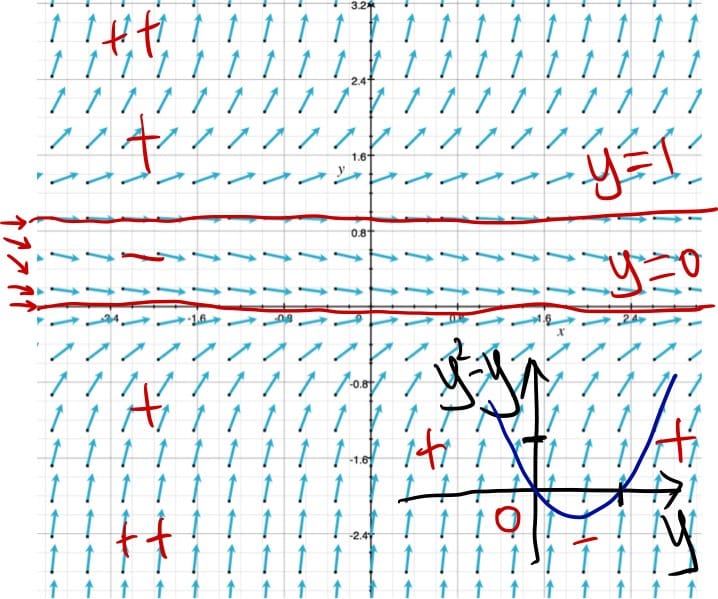
变换：可以用于任何函数，通过这种方法可以对函数有更直观的理解（非线性变换）。

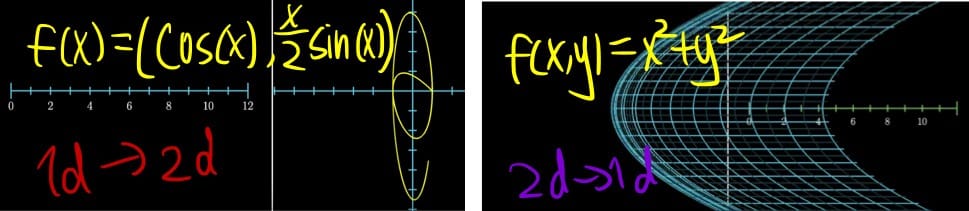
多元函数的导数

偏导数（Partial Derivatives）

In fact, this intuitive feel for the symbol is one of the most useful takeaways from single-variable calculus, and when you really start feeling it in your bones, most of the concepts around derivatives start to click. 直观的理解很重要！

$\frac{\partial f}{\partial x}$（”$\partial$” 读作：/del/ or partial）：tiny change of $f$ with respect to tiny change of $x$

直观的理解之「每个方向对函数值的贡献」

直观的理解之「在某个方向上的变化率」

梯度和方向导数（Gradient & Directional Derivatives）

方向导数：是某个方向（任意方向）上的导数，是一个数！$\nabla_{\vec{v}\ }f(x_0,y_0)= \nabla f(x_0,y_0)\cdot \vec{v}$（点积）表示为在 $(x_0,y_0)$ 上沿 $\vec{v}$（不一定是单位向量）方向的变化率。

可以仔细观察一下偏导和方向导数的定义式：

$$\frac{\partial f}{\partial x}(\vec{a})=\lim\limits_{h\rightarrow0}\frac{f(\vec{a}+h\hat{i})-f(\vec{a})}{h}$$

$$\nabla_{\vec{v}\ }f(\vec{a})=\lim\limits_{h\rightarrow0}\frac{f(\vec{a}+h\vec{v})-f(\vec{a})}{h}$$

方向导数的几何意义

梯度：是一个矢量（向量），它所在方向（最陡峭的方向）的方向导数最大，表示为 $\nabla f = \left[\begin{aligned}\frac{\partial}{\partial x}\\frac{\partial}{\partial y}\end{aligned}\right]$（可以读：nabla, del, grad）。

注意梯度的方向在底部平面上，即用 xy 平面上的一个向量表示方向

每个方向都有方向导数

$\nabla$ 可以看作是一个操作算子（Operator），其输入和输出均是函数 $f$，与 $\frac{d}{dx}$、$\frac{\partial}{\partial x}$ 类似。

其他问题：

计算方向导数时要不要将向量归一化？

If the directional derivative is used to compute slope, either $\vec{v}$ must be a unit vector or you must remember to divide by $||\vec{v}||$ at the end. Then you will get $\nabla_{\vec{v}\ }f(\vec{x})=\lim\limits_{h\rightarrow0}\frac{f(\vec{x}+h\vec{v})-f(\vec{x})}{h||\vec{v}||}$.
However, this definition puts too much emphasis on the particular use case of finding slope, so I (not me…) prefer to use the original definition and normalize $\vec{v}$ when necessary.

为什么只有一个最大值（方向导数）？

梯度定义中有「一阶连续偏导」的条件，其意味着可微，也就意味着 $f(x,y)$ 在各个方向的切线都在同一个平面上，即切平面。

梯度与方向导数有这样的关系：

$$\nabla_{\vec{v}\ }f(a,b)=\nabla f(a,b)\cdot \vec{v}$$

其中 $\nabla f(a,b)$ 是梯度。如 $\vec{v}$ 是与梯度同方向的单位向量，则方向导数取值最大，用公式可以表示为：

$$\max_{||\vec{v}||=1}\nabla f(a,b)\cdot \vec{v}$$

根据点积的几何意义（投影）可知最大值只有一个，即在两个向量的方向相同的时。

对参数曲线微分❓（Differentiating Parametric Curves）

直接上图看几何意义：

多元链式法则（Multivariable Chain Rule）

求导步骤示意图

已知：

$$\vec{v}(t)=\left[\begin{aligned}x(t)\y(t)\end{aligned}\right]、\vec{v}’(t)=\frac{d\vec{v}}{dt}=\left[\begin{aligned}\frac{dx}{dt}\\frac{dy}{dt}\end{aligned}\right]$$

$$f = f(\vec{v}(t))=f(x(t),y(t))、\frac{df}{d\vec{v}}=\nabla{f}=\left[\begin{aligned}\frac{\partial{f}}{\partial{x}}\\frac{\partial{f}}{\partial{y}}\end{aligned}\right]$$

则有：

$$\begin{aligned}\frac{df}{dt}&=\frac{d}{dt}f(x(t),y(t))=\nabla{f}\cdot\vec{v}’(t)=\left[\begin{aligned}\frac{\partial{f}}{\partial{x}}\\frac{\partial{f}}{\partial{y}}\end{aligned}\right]\cdot\left[\begin{aligned}\frac{dx}{dt}\\frac{dy}{dt}\end{aligned}\right]\&=\frac{\partial{f}}{\partial{x}}\cdot\frac{dx}{dt}+\frac{\partial{f}}{\partial{y}}\cdot\frac{dy}{dt}\end{aligned}$$

几何意义：上面的 $\nabla{f}\cdot\vec{v}’(t)$ 可以写成 $\nabla_{\vec{v}’(t)\ }f(\vec{v})$，即 $f$ 在 $\vec{v}’(t)$ 方向上的方向导数。

多元链式法则的几何意义

正规的定义式：（对比方向导数的定义式）

$$\begin{aligned}\lim\limits_{h\rightarrow0}\frac{f(\vec{v}(t+h)-f(\vec{v}(t))}{h}&=\lim\limits_{h\rightarrow0}\frac{f(\vec{v}(t)+\frac{d\vec{v}(t)}{dt}h + o(h))-f(\vec{v}(t))}{h}\&=\nabla_{\vec{v}’(t)\ }f(\vec{v})\end{aligned}$$

其它概念

曲率（Curvature）

how to describe how much you turn?

什么是曲率：用来描述曲线（在平面、空间上）弯曲程度的量。曲率越大，表示曲线的弯曲程度越大。表示为：$\kappa=||\frac{dT}{d\vec{s}}||$，其中 $T$ 为改变的弧度、$\vec{s}$ 为改变的弧长。

几何意义：马住，有点难！

一般式：$\kappa = \frac{|x’(t)y’’(t)-y’(t)x’’(t)|}{[x’(t)^2+y’(t^2)]^{\frac{3}{2}}}$。对于圆有：$\kappa = \frac{1}{R}$。

螺旋线（Helix）：

对应的函数为：$\vec{s}(t)=\left[\begin{aligned}\cos&(t)\\sin&(t)\\frac{t}{5}\end{aligned}\right]$；求导得：$\frac{d\vec{s}(t)}{dt}=\left[\begin{aligned}-\sin&(t)\\cos&(t)\\frac{t}{5}\end{aligned}\right]$

单位切线向量（Unit tangent vector）：$T(t)=\frac{\vec{s}’(t)}{||\vec{s}’(t)||} = \left[\begin{aligned}\frac{-\sin(t)}{\sqrt{26}/5}\\frac{\cos(t)}{\sqrt{26}/5}\\frac{t/5}{\sqrt{26}/5}\end{aligned}\right]$；求导得：$\frac{dT(t)}{dt}$

最后求得：$\kappa=||\frac{dT}{d\vec{s}}||=||\frac{dT/dt}{d\vec{s}/dt}||$，代入即可。

散度（Divergence）

粒子在流动

适用函数：2D → 2D、3D → 3D。

定义：是向量分析中的一个向量算子，将向量空间上的一个向量场对应到一个标量场上。对于函数 $\vec{v}(x,y)=\left[\begin{aligned}P(x,y)\ Q(x,y)\end{aligned}\right]$，其散度为 $\rm{div}\ \vec{v}=\frac{\partial{P}}{\partial{x}}+\frac{\partial{Q}}{\partial{y}}$。

写法上的Trick： $\nabla\cdot\vec{v}=\left[\begin{aligned}\frac{\partial}{\partial{x}}\ \frac{\partial}{\partial{y}}\ \frac{\partial}{\partial{z}}\end{aligned}\right]\cdot\left[\begin{aligned}P\ Q\ R\end{aligned}\right]$

几何上的意义：如First Component「即 $P(x,y)$」小于 $0$，则从左到右来看向量所指的方向往左边去一点：）

旋度（Curl）

Curl measures the rotation in a fluid flowing along a vector field. Formally, curl only applies to 3D, but here we cover the concept in 2D to warmup.

2D 下不正式的旋度计算：

3D 下的定义：可以表示三维向量场对某一点附近的微元造成的旋转程度。向量场每一点的旋度是一个向量，称为旋度向量，可表示为（运用了Notational Trick）：

$$\begin{aligned}\rm{curl}\ \vec{v} &= \nabla\times\vec{v}=\left[\begin{aligned}\frac{\partial}{\partial{x}}\ \frac{\partial}{\partial{y}}\ \frac{\partial}{\partial{z}}\end{aligned}\right]\times\left[\begin{aligned}P\ Q\ R\end{aligned}\right]=det\left(\begin{array}\
\hat{i} & \hat{j} & \hat{k} \
\frac{\partial}{\partial{x}} & \frac{\partial}{\partial{y}} & \frac{\partial}{\partial{z}} \
P & Q & R
\end{array}\right)\
&= (\frac{\partial{R}}{\partial{y}}-\frac{\partial{Q}}{\partial{z}})\hat{i} + (\frac{\partial{P}}{\partial{z}}-\frac{\partial{R}}{\partial{x}})\hat{j} + (\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}})\hat{k}
\end{aligned}$$

还需要沿着 z 轴复制多份

Interesting：旋度向量的大小等于改点上角速度的两倍。

拉普拉斯算子（Laplacian）

定义：是由欧几里得空间中的一个函数的梯度的散度给出的微分算子。

先看看 2D 下二阶导的情况：

公式和几何意义：

调和函数：一个二阶可导的函数，其满足拉普拉斯方程，即满足：$$\frac{\partial^2{f}}{\partial{x_1^2}}+\frac{\partial^2{f}}{\partial{x_2^2}}+\cdots+\frac{\partial^2{f}}{\partial{x_n^2}}=0$$

上式也经常写作：$\nabla^2f =0$ 或 $\Delta{f}=0$。

所以，当 $f’’ = 0$ 时，该点的值与其附近的点的平均值相等；当 $f’’ > 0$ 时，附近的点的平均值大于该点的值；当 $f’’ < 0$ 时，附件的点的平均值小于该点的值。

雅克比矩阵（Jacobian Matrix）

雅可比矩阵的重要性在于它体系那了一个可微方程与给出点的最优线性逼近，因此，雅可比矩阵类似于多元函数的导数。

给出 $f(\left[\begin{aligned}x\ y\end{aligned}\right])=\left[\begin{aligned}f_1(x,y)\ f_2(x,y)\end{aligned}\right]=\left[\begin{aligned}x + \sin(y)\ y+\sin(x)\end{aligned}\right]$，其对应的非线性变化如下图所示。

在以红点为原点的切空间中，该区域可以看成是局部线性的（Locally Linear）。该空间内的变换可以看成是线性变换，其变换矩阵如下：

$$\left[
\begin{array}\
\frac{\partial{f_1}}{\partial{x}} & \frac{\partial{f_1}}{\partial{y}}\
\frac{\partial{f_2}}{\partial{x}} & \frac{\partial{f_2}}{\partial{y}}
\end{array}
\right]$$

其中：第一列对应了x nudge的变化、第二列对应了y nudge的变化、$f_1$ 对应了水平方向上的移动、$f_2$ 对应了垂直方向上的移动。

多元导数的应用

局部线性化逼近（Local Linearization）

The idea is to approximate a function near one of its inputs with a simpler function that has the same value at that input.

2D 下的几何意义：如何控制这个切平面，如图所示。

令 $\vec{v} = \left[\begin{aligned}x\ y\end{aligned}\right]$、$\vec{v}_0 = \left[\begin{aligned}x_0\ y_0\end{aligned}\right]$，该切平面可以表示为（可以扩展至更高维）：

$$\begin{aligned}L_f(x,y)&=f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)+f(x_0,y_0)\
&= \nabla{f(\vec{v}_0)}\cdot(\vec{v}-\vec{v}_0) + f(\vec{v}_0)
\end{aligned}$$

局部二次非线性逼近（Quadratic Approximations）

“Quadratic” means product of two variables. $x_0$ is read “x naught”.

可以根据形如 $Q(x,y)=a+bx+cy+dx^2+exy+fy^2$ 去推导，要近似点要满足如下条件：

函数值相等，$f(x,y)=Q(x,y)$
一阶偏导都相等，$f_x=Q_x$、$f_y=Q_y$
二阶偏导都相等，$f_{xx}=Q_{xx}$、$f_{yy}=Q_{yy}$、$f_{xy}=Q_{yx}$

我就直接丢公式了（相当于线性逼近的扩展）：

$$\begin{aligned}Q(x,y)&=f(x_0,y_0) + f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)\
&+\frac{1}{2}f_{xx}(x_0,y_0)(x-x_0)^2+f_{xy}(x_0,y_0)(x-x_0)(y-y_0)\
&+\frac{1}{2}f_{yy}(x_0,y_0)(y-y_0)^2\end{aligned}$$

海森矩阵（Hessian Matrix）：

$$H_f = \left[\begin{array}\
\frac{\partial^2{f}}{\partial{x^2}} & \frac{\partial^2{f}}{\partial{x}\partial{y}}\
\frac{\partial^2{f}}{\partial{y}\partial{x}} & \frac{\partial^2{f}}{\partial{y^2}}
\end{array}\right]$$

包装了关于函数 $f$ 的所有二阶偏导，还可以扩展到更高维。

用途：局部二次非线性逼近（方便向量化）、其行列式用于二次偏导检测

向量化：

我们用 $\vec{v}$ 表示 $[x, y]$，$\vec{v}_0$ 表示 $[x_0, y_0]$，则有

$$\begin{aligned}\
Q(\vec{v})&=f(x_0,y_0) + \left[\begin{array}\ f_x(x_0)\ f_y(y_0)\end{array}\right]\cdot\left[\begin{array}\x-x_0\y-y_0\end{array}\right] + [x-x_0\ y-y_0]\left[\begin{array}\ \frac{1}{2}f_{xx} & \frac{1}{2}f_{xy}\ \frac{1}{2}f_{yx} & \frac{1}{2}f_{yy}\end{array}\right]\left[\begin{array}\ x-x_0\ y-y_0\end{array}\right]\
&=f(\vec{v}_0) + \nabla{f(\vec{v}_0)}\cdot(\vec{v}-\vec{v}_0) + \frac{1}{2}(\vec{v}-\vec{v}_0)^{T}H_f(\vec{v}-\vec{v}_0)
\end{aligned}$$

总结的一些对应关系：

一元：$\frac{df}{dx}$、$\frac{d^2f}{dx^2}$、$\frac{d^3f}{dx^3}$、…
多元：$\nabla{f}$、$H_f$、$\cal{Multilinear\ Algebra}$❓

多元函数的最优化（Optimizing Multivariable Functions）

鞍点（Saddle Points）：在微分方程中，沿着某一方向是稳定的，另一方向是不稳定的奇点，或者不是局部极值点的驻点「neither maxima nor minima」。从不用角度看该点，可以同时具有局部极大值和局部极小值。

二阶偏导测试（Second Partial Derivative Test）：

我们可以用二级导数来判定某个点是否为鞍点。从上图看二阶导数一正一负，不能判断为局部极值点。当出现 $\nabla{f}(x_0,y_0)=0$ 时（Critical Point），我们用以下式子判断是否出现鞍点：

$$\cal{H}=f_{xx}(x_0,y_0)\ f_{yy}(x_0,y_0)-f_{xy}(x_0,y_0)^2$$

若 $\cal{H}>0$，则该点是局部极值点；若 $\cal{H}<0$，则该点是鞍点；若 $\cal{H}=0$，无法判断。

其中，$\cal{H}=0$ 的情况与下图的情况类似：

进一步思考：

$$f(x)\approx f(a)+f’(a)(x-a)+\frac{1}{2}f’’(a)(x-a)^2$$

当 $f’(a)=0$ 时，$f(x)\approx f(a)+\frac{1}{2}f’’(a)(x-a)^2$，因为 $(x-a)^2\geq 0$，所以 $f’’(a)$ 可以决定局部极小值和局部极大值。
当 $f’(a)=0$、$f’’(a)=0$ 时，$f(x)\approx f(a)$ 得到的是一个常量，无法决定是局部极大值还是局部极小值。

拉格朗日乘子法和约束优化（Lagrange Multipliers $\lambda$ and Constrained Optimization）

举个例子：

收入（Revenue）：$R(x,y)=x^2e^yy$
预算/成本（Budget）：$B(x,y)=x^2+y^2$

约束问题可以表述：

$$\max{R(x,y)=x^2e^yy},\
\rm{s.t.\ }\mit{B}(x,y)=x^2+y^2=b$$

解决该问题的本质是找到 $R(x,y)$ 与 $B(x,y)$ 的等高线相切的点，如下图所示。当 $B(x,y)=b$ 时，红色圆是固定不变，可以调整 $R(x,y)$ 的大小以获得能够满足相切情况的等高线。

红线为 B

相切的情况意味着梯度方向相同或者相反：$\nabla{R}=\lambda\nabla{B}$，结合以上三个式子就可以求出最优解。

为了方便计算机计算，我们可以用一个式子表达上述的约束问题：

Constrained Problem → Unconstrained Problem（计算机擅长这个）

$\lambda$ 有什么含义：

将 $M^*$ 看成是 $b$ 的函数有 $M^*(b)=R(x^*(b),y^*(b))$，此时 $x^*(b)$ 和 $x^*(b)$ 是隐式函数。此时，我们可以得出 $\lambda^*=\frac{dM^*}{db}$，即 $M^*(b)$ 对于微小变化 $b$ 的变化率为 $\lambda^*$。

这说明：如果 $\lambda^* > 0$，说明我们可以使 $b$ 变大，从而使得 $M^*$ 变大，具有应用价值（或者提高一点点 $b$，可以得到大概的变化量！）。

证明（Proof）：

$\cal{L}^*$ 和 $\cal{L}$ 不同，前者是四元函数（包含 $b$），后者是三元函数。

$$\cal{L}^*(x^*(b),y^*(b),\lambda^*(b),b)=R(x^*(b),y^*(b))-\lambda^*(B(x^*(b),y^*(b))-b)$$

$$\frac{d\cal{L}^*}{db}=\frac{\partial{\cal{L}^*}}{\partial{x}}\cdot \frac{dx^*}{db} + \frac{\partial{\cal{L}^*}}{\partial{y}}\cdot \frac{dy^*}{db} + \frac{\partial{\cal{L}^*}}{\partial{\lambda}}\cdot \frac{d\lambda^*}{db} + \frac{\partial{\cal{L}^*}}{\partial{b}}\cdot \frac{db}{db}$$

其中：$\frac{\partial{\cal{L}^*}}{\partial{x}}$、$\frac{\partial{\cal{L}^*}}{\partial{y}}$、$\frac{\partial{\cal{L}^*}}{\partial{\lambda}}$ 均为 $0$（原因：看看上面图左边的公式），所以原式如下

$$\frac{d\cal{L}^*}{db}=\frac{\partial{\cal{L}^*}}{\partial{b}}=\lambda^*(b)$$

多个条件：马住❗️

条件为不等式：马住❗️

KKT 条件：马住❗️