微积分探讨的三大思想:
Integrals 积分 $\int^R_0$
Derivatives 求导 $\frac{d}{dx}$
Fact that they are opposite 它们的关系
当你使用 $dt$ 时,你只是想表示 $dt\rightarrow 0$,它既不是「不穷小」,也不是 $0$。
$a^t$ 可以表示为 $e^{ct}$,其中$c=\ln a$。为什么选用 $e$ 而不是其他底?
$a^{kt} = k \times \ln a\times a^{kt}$ (多了 $\ln a$)
$e^{kt} = k \times e^{kt}$ ($k$ 即为变化率)
符合自然中的许多现象,变化率总是和变化量成正比:
人口增长
温度变化
金钱投资
位移 $s(t)$ 的导数:
$\frac{ds}{dt}$ Velocity
$\frac{d^2s}{dt^2}$ Acceleration
$\frac{d^3s}{dt^3}$ Jerk(急动度)
Chain Rule 的直观理解:
![]()
- 泰勒展开式每一项的系数可以看作是一种
控制:
![]()
- 夹逼定理(Squeeze Theorem)
$$g(x) \leq f(x) \leq h(x)$$
$$\left{
\begin{aligned}
\lim\limits_{x\rightarrow a} g(x)=L \
\lim\limits_{x\rightarrow a} h(x)=L
\end{aligned}
\rightarrow \lim\limits_{x\rightarrow a} f(x)=L
\right.$$
![]()
连续性
定义:设函数 $y=f(x)$ 在点 $x_0$ 的某一领域内有定义,如果$$\lim\limits_{\Delta x \rightarrow 0}\Delta y = \lim\limits_{\Delta x \rightarrow 0}[f(x_0 + \Delta x) - f(x_0)]=0,$$
那么称 $y=f(x)$ 在点 $x_0$ 上连续。
函数极限的性质
唯一性
有界性:如果 $\lim\limits_{x \rightarrow x_0}f(x)=A$,则存在常数 $M > 0$ 和 $\delta > 0$,使得当 $0 < |x - x_0| < \delta$ 时,有 $|f(x)|\leq M$
局部保号性
无穷小(Infinitesimal or Infinitely Small)
定义:如果 $f(x)$ 当 $x\rightarrow x_0$(或 $x\rightarrow \infty$)时的极限为 $0$,那么称 $f(x)$ 为当 $x\rightarrow x_0$(或 $x\rightarrow \infty$)时的无穷小。不要把它和很小的数混为一谈!
无穷大(也不是数,只是极限趋于无穷大)
无穷小的比较 → 反映了不同的无穷小
趋近的快慢:$\lim \frac{\beta}{\alpha} = 0$,$\beta$ 比 $\alpha$ 高阶的无穷小,记为 $\beta=o(\alpha)$
$\lim \frac{\beta}{\alpha} = \infty$,$\beta$ 比 $\alpha$ 低阶的无穷小
$\lim \frac{\beta}{\alpha} = c \neq 0$,同阶无穷小
$\lim \frac{\beta}{\alpha^k} = c \neq 0$,$\beta$ 是 $\alpha$ 的 $k$ 阶无穷小
$\lim \frac{\beta}{\alpha}=1$,等价无穷小,记为 $\alpha \sim \beta$
定理 1:$\beta$ 与 $\alpha$ 是等价无穷小的充要条件为 $\beta=\alpha+o(\alpha)$。
当 $x \rightarrow 0$ 时,$\sin(x) \sim x、\tan(x)\sim x、\arcsin(x)\sim x、1-\cos(x)\sim\frac{1}{2}x^2$
定理 2:设 $\alpha \sim \alpha’,\beta \sim \beta’$,且 $\frac{\lim \beta’}{\lim \alpha’}$ 存在,则 $\lim \frac{\beta}{\alpha} = \lim \frac{\beta’}{\alpha’}$。
不连续点或间断点
满足三种情况之一:
在 $x=x_0$ 没有定义
在 $x=x_0$ 有定义,但在 $\lim\limits_{x\rightarrow x_0}f(x)$ 不存在
在 $x=x_0$ 有定义,但 $\lim\limits_{x\rightarrow x_0}f(x) \neq f(x_0)$
一类间断点(左右极限存在)
可去间断点(极限相等)
跳跃间断点(极限不相等)
二类间断点(左右极限不存在)
无穷间断点
振荡间断点
区分「微分 Differential」和「导数 Derivative」
微分的定义:设 $y=f(x)$ 在某区间内有定义,增量 $\Delta y = f(x_0 + \Delta x)-f(x_0)$ 可以表示为 $\Delta y = A\Delta x + o(\Delta x)$,其中 $A$ 是不依赖于 $\Delta x$ 的常数「$A=f’(x)$」,那么称 $f(x)$ 在 $x =x_0$ 上是可微的,则 $A\Delta x$ 也叫作改点上的微分,记作 $dy$,即 $dy = A\Delta x$。几何意义:切线的一元线性方程。局部切线段近似代替曲线段,即非线性函数的局部化。
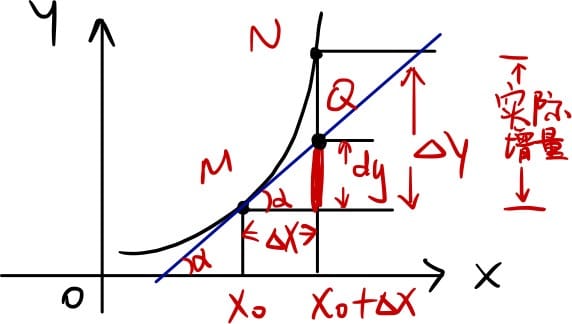
导数是函数到函数的映射,而微分是求另一个与导函数有关的函数。对于一元函数可能看不出什么区别,但对于二元函数,没法同时对 $x$ 和 $y$ 求导,但可以同时对它们求微分。比如在工程中常用:
$$\Delta y = f(x_0 + \Delta x) - f(x_0) \approx f’(x_0)\Delta x$$
如 $\sqrt[n]{1+x}\approx 1+\frac{1}{n}x$、$e^x \approx x$。
- 全微分:$\Delta z =f(x+\Delta x, y+\Delta y) - f(x,y) = \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y + o(\sqrt{(\Delta x)^2+(\Delta y)^2})$
微分中值定理
- 条件:
- 在 $[a, b]$ 上连续
- 在 $(a, b)$ 上可导
- 不同❓
罗尔定理:至少有一点 $f’(\xi)=0$
拉格朗日中值定理:$\frac{f(b)-f(a)}{b-a}=f’(\xi)$
柯西中值定理:$\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f’(\xi)}{F’(\xi)}$,当 $\left{\begin{aligned} X=F(x)\Y=f(x) \end{aligned} \right.(a \leq x \leq b)$
- 条件:
泰勒中值定理
- 如果函数 $f(x)$ 在含有 $x_0$ 的某个区间 $(a,b)$ 内具有直到 $(n+1)$ 阶的导数,则对任一 $x\in(a,b)$ 有:
$$f(x)=f(x_0)+f’(x_0)(x-x_0)+\frac{f’’(x_0)}{2!}(x-x_0)^2 + \dots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x)$$
其中 $R_n(x) = \frac{f^{(n+1)}(x_0)}{(n+1)!}(x-x_0)^{n+1},(x_0 \leq \xi \leq x)$,为拉格朗日型余项;而 $R_n(x) = o[(x-x_0)^n]$ 为佩亚诺型余项。
函数凹 / 凸
$f(\frac{x_1+x_2}{2}) < \frac{f(x_1)+f(x_2)}{2} \Leftrightarrow f’’(x) > 0$ (凹,极小值)
$f(\frac{x_1+x_2}{2}) > \frac{f(x_1)+f(x_2)}{2} \Leftrightarrow f’’(x) < 0$ (凸,极大值)
$f’’(x) = 0$ 对应的点称为拐点(Inflection Point),凹凸都有可能。
换元积分法
第一类:设 $f(u)$ 具有原函数,$u=\varphi(x)$ 可导,则有换元公式$$\int f[\varphi(x)]\varphi’(x)dx = [\int f(u)du]_{u=\varphi(x)}$$
第二类:$$\int f(x)dx = \int f[\psi(t)]\psi’(t)dt$$
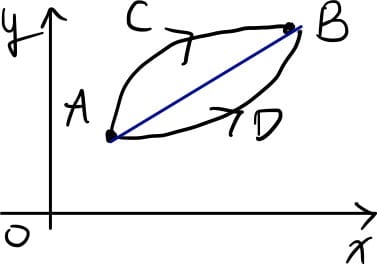
定积分中值定理
如果函数 $f(x)$ 在积分区间 $[a,b]$ 上连续,则在 $[a,b]$ 上至少存在一个点 $\xi$,使下式成立:$$\int^b_a f(x)dx=f(\xi)(b-a),(a \leq \xi \leq b)$$
$f(\xi)$ 是平均值。
微分方程
定义:表示未知函数($y$)、未知函数的导数($\frac{dy}{dx}$)与自变量($x$)之间的关系的方程,如 $\frac{dy}{dx}=2xy$、$x^3y’’’=3x^2$。
求解:如上面方程通过变量分离后得 $\frac{dy}{y}=2xdx$,再对两端积分得 $y=\pm e^{x^2+C_1}$。
平面及其方程
三元方程:$F(x,y,z)=0$
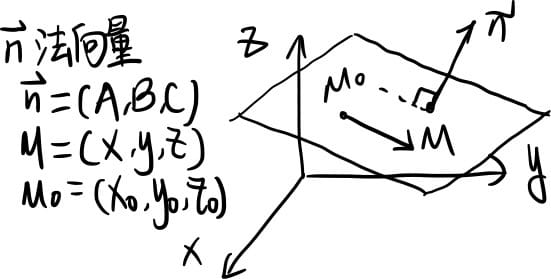
平面点法式方程:$\vec{n}\cdot\overrightarrow{M_0 M} = 0 \Leftrightarrow A(x-x_0)+B(y-y_0)+C(z-z_0)=0$
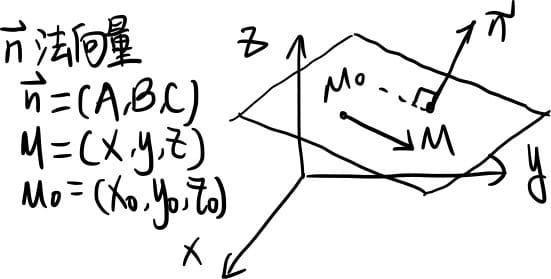
一般方程:$Ax+By+Cz+D=0,\vec{n}=(A,B,C)$
截距式方程:$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
空间直线及其方程
一般方程:$\left{\begin{aligned}A_1x+B_1y+C_1z+D_1=0\A_2x+B_2y+C_2z+D_2=0\end{aligned}\right.$
对称式方程(点向式方程):$\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}$
参数方程:$\left{\begin{aligned}x&=x_0+mt\y&=y_0+nt\z&=z_0+pt\end{aligned}\right.$
空间曲线及其方程
一般方程:$\left{\begin{aligned}F(x,y,z)=0\G(x,y,z)=0\end{aligned}\right.$
参数方程:$\left{\begin{aligned}x=x(t)\y=y(t)\z=z(t)\end{aligned}\right.$